The Engine Iceberg Looms Larger

Last week's post, An Engine Iceberg (November 2021), looked at runtime data from 'TCEC C960 FRC3', which I covered on this blog in March 2021. I wrote,

Since the data covers only the first move of 25 SPs (50 games) out of the full set of 960 SPs, it's obviously just scratching the surface. Suppose we had data for the first few moves of all 960 SPs from many different engines played over a long period of time. What might we learn from this?

For this current post I repeated the exercise on the final match of the CCC C960 Blitz Championship (October 2021). I wrote,

In the final match Stockfish beat Dragon +10-1=589. Yes, more than 98% of the final games were drawn.

I loaded the PGN for all 600 games into my database and ran a preliminary analysis. There were two small surprises.

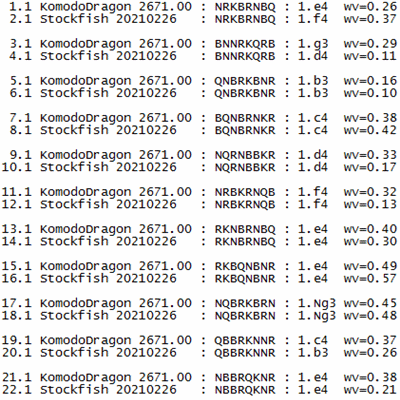
The first surprise was that the data for individual moves was not the same for both the TCEC and the CCC. Here are examples for the first move of the first game in both events.

TCEC: 1. e4 {d=36, sd=36, mt=147236, tl=1657764, s=81363821, n=11979602252, pv=e4 Nb6 Nb3 e5 g3 g6 Ne3 c6 f4 exf4 gxf4 f5 exf5 gxf5 Bf2 Qf6 c3 Nd5 Bc2 Nxe3 Qg1 Ne6 Bxe3 Bc7 O-O-O O-O-O Nd4 Bf7 Rf1 Bh5 Rde1 Nxd4 Bxd4 Qf7 b3 Be2 Rf2 Bg4 Kb2 Rxe1 Qxe1 Rg8 Qf1 Bb6 Bxb6, tb=0, h=99.9, ph=0.0, wv=0.26, R50=50, Rd=-11, Rr=-1000, mb=+0+0+0+0+0,}

CCC: 1. d4 {+0.45/32 9.6s, ev=0.45, d=32, pd=g6, mt=00:00:09, tl=00:04:55, s=148396 kN/s, n=1415409674, pv=d4 g6 e3 d5 g4 c6 c4 dxc4 f4 g5 fxg5 Na6 Nf2 e5 Bxc4 Nb4 Na3 exd4 Qf3 Be7 exd4 Qxd4 O-O O-O Bb3 Ne6 h4 Qg7 Be3 Nd5 Ne4 Nxe3 Qxe3 h6 Nc4 hxg5 Ncd6, tb=0, R50=50, wv=0.45}

Fortunately, the important 'wv' and 'pv' fields are available for both events. Any other fields I decide to use might require some sort of conversion.

The second surprise was that the CCC start positions (SPs) were not repeated for a second game, colors switched, between the engines. Instead, a new SP was assigned to each game. The left table in the following chart shows that some SPs were nevertheless repeated up to five times.

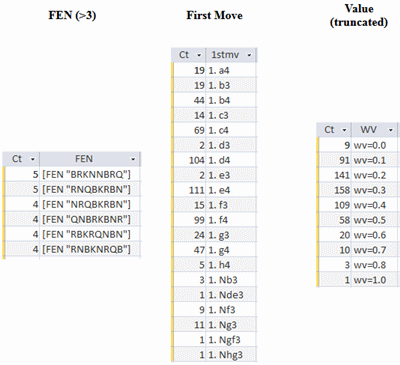
In addition to the six SPs shown in the table, 24 SPs were repeated three times and 90 were repeated twice. I assume that the SPs are chosen randomly for both the TCEC and the CCC, perhaps with the exception of SP518 RNBQKBNR, but I know from past investigations that several bad algorithms are in use elsewhere; see Start by Placing the Bishops (September 2017) for examples.

The center table in the chart shows the number of times a certain first move was chosen across all 600 games. For example, the initial moves 1.a4 and 1.b3 were both chosen 19 times. Just as in SP518, advancing a center Pawn two squares (1.c4, 1.d4, ...) is the most popular opening strategy. Although any single SP has a maximum of four initial Knight moves, sometimes only two or three moves, all eight moves are possible across the 960 SPs.

There are a number of questions for further exploration. When is the advance of an edge Pawn -- 19 x 1.a4 or 5 x 1.h4 -- desirable? I suspect these are position where the Queen starts in the corner behind the Pawn. Why the large difference between the counts on the two edge Pawns? Perhaps this is because of castling O-O/O-O-O considerations. Also worth noting is that O-O/O-O-O was never chosen for the first move.

The rightmost table in the chart gives a rough distribution of initial 'wv' values, i.e. what value did the engine calculate for its first move? These are truncated values, e.g. the CCC 'wv=0.45' shown above is counted in the table as 'wv=0.4'. I could have used roundoff and a bar chart to display the counts more accurately, but I ran out of time.

One big question presents itself here. Why are there so many 'wv' greater than 0.5, but so few decisive results during the match? I also need to determine if Stockfish and Dragon calculate values in the same statistical range. I doubt that they do.

The three tables in that chart lead to many questions and few answers. I'll take this up again some other time.

An Engine Iceberg

In the previous post, CCC C960 Blitz Championship (October 2021), I wrote,

Given that engines' evaluations for every move are available in the event's PGN game scores, perhaps there is something to be learned about the 960 different start positions. That investigation would make a good follow-up post.

Make that two good follow-up posts. The first post was on my main blog, Evaluating the Evaluations (November 2021), where I concluded,

Now that I have a tool for rapidly evaluating the engine evaluations, what can I do with it? The first task will be to put it to work on the 960 start positions used in chess960.

The second post is this one. I had already downloaded a few PGN files from recent engine vs. engine events, so the first question was which one to use. I decided to continue with the games from an event that I covered earlier this year in another post on this blog, TCEC C960 FRC3 (March 2021). At that time I noted,

Except for an occasional CCRL game, I can't remember ever looking at an engine vs. engine chess960 game. Is there anything to be learned from such an exercise, or is the play of the engines beyond comprehension?

TCEC FRC3 was a 50 game match won by KomodoDragon over Stockfish on a final score of +2-1=47. The seven mandatory tags in the PGN header for the first game look like this:-

[Event "TCEC Season 20 - FRC3 Final"]
[Site "https://tcec-chess.com"]
[Date "2021.03.14"]
[Round "1.1"]
[White "KomodoDragon 2671.00"]
[Black "Stockfish 20210226"]
[Result "1/2-1/2"]

I loaded the file into my database, added the concept of SP, and produced the following chart. It covers the first 22 games of the match. Each start position (SP) was played twice, where KomodoDragon always had White in odd-numbered games. In a match between humans, this pattern would risk giving an advantage to one of the players, but in games between engines, it's harmless.

The last two columns show the first move, as chosen by White, and the value ('wv') calculated by the engine for that move. I could have also shown the principal variation ('pv') calculated by White, but that wouldn't add much to an initial understanding of the data. The same data is available from the PGN file for all moves by both sides in a game.

Since the data covers only the first move of 25 SPs (50 games) out of the full set of 960 SPs, it's obviously just scratching the surface. Suppose we had data for the first few moves of all 960 SPs from many different engines played over a long period of time. What might we learn from this? I would want an answer to that question before spending too much effort collecting more data.